Selon cette définition strictement formel de la technologie de production et de la fonction de production, nous allons revenir à l’illustration graphique de la fonction de production ..Mais à quoi ressemblerait une version purement graphique de la fonction de production ? Et que dire de la représentation mathématique de la fonction de production? Quels types de fonctions sont utilisées pour représenter les fonctions de production?
La loi des rendements marginaux décroissants
Nous allons d’abord jeter un oeil à la représentation graphique d’une fonction de production.
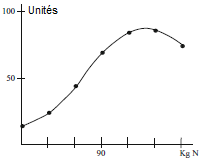
Rappelons que la fonction de production ne peut être tirée sur un morceau de papier s’il y a un ou le maximum deux intrants. Comme plus de deux entrées sont normalement utilisées dans une production, (presque) toutes les illustrations graphiques des fonctions de production supposent la présence d’une ou plusieurs entrées sous-jacents (partie de la production) avec des montants fixes données (entrée fixe). La courbe illustrant la relation entre l’engrais azoté ajoutée et le rendement des cultures céréalières dans la figure, par conséquent, suppose que tous les autres intrants utilisés dans la production de cultures de céréales (semences, pesticides, la terre, la main-d’œuvre, machines, etc.) sont présents en quantités fixes données.
Une condition préalable essentielle liée à une fonction de production est l’hypothèse de rendements marginaux décroissants. La condition préalable, qui est basée sur des observations empiriques de la façon dont la production est réalisée dans la pratique, est universellement reconnu comme une condition de base au sein de l’économie de production dénommée la loi des rendements décroissants marginaux. Brièvement expliqué,
La loi des rendements marginaux décroissants stipule qu’en ajoutant des quantités croissantes d’entrée à une production d’au moins une entrée fixe, les rendements supplémentaires résultant de l’addition de quantités croissantes de l’entrée diminuera graduellement, et finalement devenir négative.
Le concept de rendement marginal est utilisé ici pour se référer à l’augmentation de la production résultant de l’ajout d’une unité supplémentaire de l’entrée. Normalement, cette augmentation est exprimée par la pente de la fonction de production, à savoir que la valeur de la dérivée, soit df (x) / dx, si x est un scalaire, ou la dérivée partielle, ∂f (x) / ∂xi, si x est un vecteur. Exprimé de cette façon, la notion de rendements marginaux ou produit marginal est normalement utilisé pour exprimer les rendements supplémentaires par unité d’entrée en relation avec des changements marginaux dans la quantité d’entrée.
Si l’expression de la fonction de production est inconnue, le produit marginal peut être approchée par l’utilisation du produit de la différence, exprimée en dy / dx. En utilisant des données à partir des valeurs de la courbe ci-dessus, le produit de la différence dans l’intervalle de 30 à 60 kg d’azote est égal à (45-25) / (60-30) ¼ 0,67, et dans l’intervalle de 90 à 120 kg de quantités égales d’azote (85 à 70) / (120-90) ¼ 0,50. Cette différence de produits sont expressions approximées du dérivé (et là par le produit marginal) au centre des intervalles appropriées.
La loi de rendement marginal décroissant est bien illustrée dans la fonction de production représentée sur la figure. 2.1. Lors de l’ajout de petites quantités d’engrais azotés, le produit marginal augmente (la pente de la fonction de production augmente). À un certain point, le produit marginal diminue, et lors de l’ajout d’environ 135 kg d’azote, le produit marginal devient zéro et devient par la suite négative avec d’autres ajouts. Dans cet exemple, la condition préalable d’au moins une entrée fixe est convaincu que la terre et d’autres entrées utilisées dans la production des cultures céréalières sont pré censés être présents en quantités fixes données.
2 commentaires
Un vrai « charabia », truffé de fautes de tous types : orthographe, syntaxe, etc. Lamentable !
Etes-vous conscient de l’image qu’un tel texte véhicule ?
Au minimum, par respect pour le lecteur, faites relire par quelqu’un qui maitrise la langue française…
Merci pour votre critique.
A mon tour, je veux voir des commentaires qui respectent ce que vous demandez.