La détermination des ressources
Essentiellement, trois types de ressources de capacité sont déterminés : les besoins en nombre de machines ou équipements, en effectif ouvrier et en matières premières ou composants.
Le nombre de machines se détermine en calculant le volume de bons produits désirés par rapport à la capacité de la machine tout en prenant en considération le taux d’utilisation, le taux de défectuosité, le taux de rendement et d’autres facteurs, comme le temps de mise en route.
EXEMPLE 1 :
Le temps standard requis pour la fabrication d’une pièce B est de 2 mn. Le taux d’utilisation de la machine est de 80 %. L’opération engendre 4 % de malfaçons.
Combien de machines devrait-on employer par journée de 8 heures, pour produire 5000 unités ?
Solution :
Capacité de production de la machine : (8h * 60 mn * 80 %/2 mn) * 0.96 =184,32 unités.
Soit un nombre de machines : 5000 / 184,32 = 27.17 machines
Puisqu’une machine est indivisible, On optera pour 28 machines, soit un léger surcroît de capacité qui peut occasionner un déséquilibre de capacité surtout s’il s’agit d’un processus à plusieurs étapes.
Le calcul de l’effectif risque d’être plus complexe, car il intègre des ressources pour des opérations variées, des machines différentes, des temps de mises en route,…
En plus, il faut considérer des rendements de personnes différentes et déterminer la main d’œuvre indirecte, soit les personnes affectées à la réception, l’expédition, la manutention et l’entretien.
Le calcul des matières premières utilisées s’effectue essentiellement selon la même logique que le calcul des autres besoins. Cependant, à part la rectification des rejets, il y a lieu de tenir compte du taux de transformation matière ; soit le rapport entre les matières premières qui composent le produit et celles utilisées dans la fabrication.
EXEMPLE 2 :
. On doit fabriquer 5000 moulages d’aluminium ayant chacun un poids net de 2 kg. Pour couler ces moulages, on utilise un système d’alimentation (des conduits qui amènent le métal liquide jusqu’à l’empreinte de la pièce) et un système de masselottage (une masse de métal liquide coulée en même temps que la pièce afin de l’alimenter lors de la solidification et éviter ainsi les défauts liés au retrait). Ces deux systèmes qui sont éliminés de la pièce moulée après sa solidification, pèsent 0,75 Kg. Dans cette fonderie le taux de rejet est de 4 %.
Quelle est la quantité de métal qui doit être en fusion et quel est le taux de rendement matière ?
Solution :
Chaque bonne pièce nécessite 2 kg d’aluminium. 0,75 Kg pour l’alimentation et le masselottage, en plus d’une rectification de 4 % pour les pièces défectueuses. Soit
(2 Kg + 0,75 Kg)/ (1 – 0.04) = 2,865 kg d’aluminium / pièce
Pour 5000 pièces, on a donc besoin de 5000 unités * 2.865 Kg = 14325 Kg
Le taux de rendement matière se calcule ainsi :
Poids net / poids brut = 5000 * 2 / 14325 = 2 / 2,865 = 70 %
Plus le rendement matières n’est faible: plus la capacité doit être grande.
Les facteurs de rectification s’imposent simplement lorsqu’il s’agir d’un Processus à étape unique. Cependant, ces mêmes facteurs réduisent beaucoup la capacité d’une installation lorsqu’il y a plusieurs étapes reliées à la transformation des matières ou produits finis.
En effet, on constate que la détermination des ressources dans un contexte de multi étapes séquentielles et dépendantes exige une attention particulière d’équilibrage afin d’utiliser adéquatement la capacité. C’est l’étape la moins productive qui établit la capacité et en détermine les ressources.
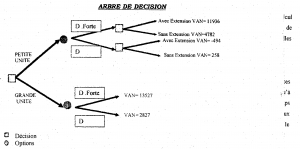
4.2- L’arbre de décision
L’arbre de décision est une représentation graphique d’une partie lorsqu’on a plusieurs choix à exercer et qu’on fait face à une incertitude quant à un évènement futur.
Ceci est particulièrement Vrai lorsqu’il s’agit de projets d’accroissement de capacité. Dans un tel contexte, la prise de décision est relativement simple : l’identification des options, l’identification des évènements futurs possibles, le calcul d’une matrice de cash-flows nets actualisés, leur pondération par les probabilités des événements et l’établissement de l’arbre de décision.
APPLICATION:
Une entreprise envisage d’élargir sa gamme de production avec un nouveau produit dont la demande est incertaine. Elle envisage de construire soit une grande unité de production (investissement initial à l’instant
0 : I0 = 15000), soit commencer par une petite unité (l0 = 10000) tout en gardant la possibilité d’une extension l’année d’après pour un coût de 6000.
La matrice des cash-flows prévisionnels a été établie par le service des études de la façon suivante :
| Demande élevée | Demande faible | |||||
| Grandeunité | Petite unité | Grandeunité | Petite unité | |||
| Avec ext. | Sans ext. | Avec ext. | Sans ext | |||
| Année I | 5000 | 3000 | 3000 | 2000 | 2000 | 2000 |
| Année 2 | 10000 | 10000 | 5000 | 10000 | 5000 | 4000 |
| Année 3 | 15000 | 15000 | 6000 | 10000 | 5000 | 4000 |
| Année 4 | 15000 | 15000 | 8000 | 10000 | 6000 | 4000 |
Sachant que, la probabilité d’une demande forte est de 70 %, celle d’une demande faible de 30 %? Calculer les valeurs actuelles nettes cash-flows issus des deux projets en considérant que l’entreprise prendra le meilleur choix en t = 1. Le coût du capital utilisé par l’entreprise (coût d’opportunité de l’argent) est de 10%.
Le traçage de l’arbre de décision permet de ne retenir que les décisions adéquates en fonction de la réalisation effective des prévisions.
Le choix se portera donc sur la grande usine.
L’utilité de l’arbre de décision reprend sous forme de graphique le calcul de la VAN. Il permet de mieux saisir le problème lorsqu’il présente une série de décisions séquentielles. L’arbre de décision permet de choisir la meilleure option lorsqu’il y a incertitude, donc risque face aux événements futurs