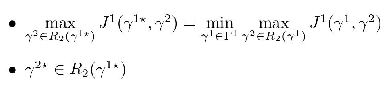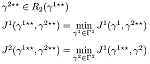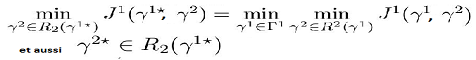On définit l’équilibre de stackelberg à l’aide d’un petit exemple. C’est un cours simple pour faciliter la compréhension de la théorie de Stackelberg,

Définition équilibre de Stackelberg

Soit Γ1 l’ensemble des stratégies pour le leader et Γ2 l’ensemble des stratégies pour le suiveur. Soit la meilleure fonction de réponse du suiveur. Une stratégie de leader γ 1? et stratégie de suivi 2? sont en équilibre de Stackelberg si les conditions suivantes sont réunies,

Théorème:  Dans une partie finie à 2 joueurs, il y a toujours un équilibre de Stackelberg dans les stratégies pures.

Preuve: Supposons un jeu où P1 est le leader et P2 est le suiveur. Puisque le jeu est fini, Γ1 et Γ2 sont finis et donc la meilleure fonction de réponse R2 pour toute stratégie γ 1 correspond à un ensemble fini non vide. Ainsi, si la stratégie d’équilibre du leader, γ sort, alors une stratégie pour le suiveur, γ 2? ∈ R2 (γ1?

De plus, dans la recherche de la stratégie d’équilibre du leader, on trouve toujours un minimum ou un maximum sur des ensembles finis non vides. Puisqu’un extremum existerait toujours sur un ensemble fini non vide, une stratégie d’équilibre de Stackelberg (γγ2) existerait toujours dans une partie finie à 2 joueurs.

Relation avec l’équilibre de Nash

Ce n’est pas nécessairement la même chose que l’équilibre de Nash. Si (γ1 ??, γ2 ??) est l’équilibre de Nash alors,

Il n’y a aucune raison pour que ceux-ci soient identiques ou liés. Cependant, comme nous le verrons plus loin, si nous mettons certaines conditions sur les meilleures fonctions de réponse ou la formulation de la stratégie de leader, nous pouvons prouver que le gain de l’équilibre de Stackelberg ne peut pas être pire que celui de l’équilibre de Nash.

Formulation optimiste de l’équilibre de Stackelberg

Supposons une partie à 2 joueurs où, Γ1 désigne l’ensemble de stratégies pour le leader et Γ2 l’ensemble de stratégies pour l’adepte. Soit R2: Γ1 → 2 la meilleure fonction de réponse du suiveur.

On dit que pour une formulation optimiste ou lorsque le leader est optimiste, l’équilibre de Stackelberg en stratégies pures (γ, γ2) existe et est tel que,

Ici, nous prenons le minimum sur toutes les stratégies suiveurs en réponse à une stratégie leader (par opposition au maximum que nous avons pris dans le cas précédent). Le leader est donc optimiste que de toutes les stratégies avec lesquelles l’adepte peut répondre, il jouerait celle qui donne au leader le meilleur gain.

Théorème 23.2 Considérons une partie finie à 2 joueurs dans le modèle de Stackelberg tel qu’un équilibre de Nash existe. Soit J le gain du leader à l’équilibre de Stackelberg et J N celui à l’équilibre de Nash.

Alors si R2 est une valeur unique ou si le leader est optimiste (pour une formulation optimiste du jeu), alors